- Barriere zwischen einem Metall und einem n-Halbleiter a) vor der
Kontaktierung, b) nach der Kontaktierung .
- Ohm'scher Metall-Halbleiter-Übergang a) bei geringer Barrierenhöhe, b)
bei hoher Dotierungskonzentration .
- Selbstkonsistentes Lösungsschema .
- Diskretisierung des kompakten Trägers der Poisson-Gleichung.
- Angenommener Leitungsbandkantenverlauf erzeugt durch eine
Oberflächenladung
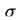 am linken Rand am linken Rand 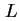 bei bei 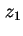 . .
- a) entkoppelte p- und n- Halbleiter, b) Raumladungszone am pn-Übergang.
- Mit (2.4) berechnete CV-Kennlinie für einen kreisförmigen
Mesa mit
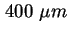 Durchmesser und einseitig-abrupten Übergang aus Silizium-dotiertem GaAs
( Durchmesser und einseitig-abrupten Übergang aus Silizium-dotiertem GaAs
(
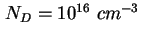 ). ).
- Experimentelle CV-Kennlinien der Proben T3189 (pn-Diode mit Quantenpunkten,
siehe Abschnitt 2.6.2) und T3191 (zugehörige Referenzprobe ohne Quantenpunkte) [Kap00b],
[Kap01].
- Harmonischer Potentialverlauf.
- Ladungsdichte
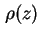 und daraus resultierende Feldstärke und daraus resultierende Feldstärke 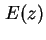 am
am 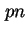 -Übergang. -Übergang.
- Zerlegung des Bauteils in zwei Leiter.
- Elektron-Energien in pyramidenförmigen InAs-Quantenpunkten
mit verschiedenen Größen, berechnet mit 8-Band k.p-Theorie und zwei verschiedenen
Verspannungsmodellen. Gestrichelte Linien verbinden Energieniveaus mit derselben Symmetrie der
Wellenfunktion [Sti99].
- Experimentelle (Symbol) und errechnete (Rot) CV-Kennlinie der Probe Z14a
[Ehe02]. Die Rechnung ergibt eine Lage der beiden Energieniveaus bei
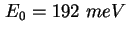 und und
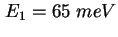 ,
mit Verbreiterungen von ,
mit Verbreiterungen von
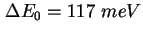 und und
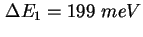 .
Das Inset zeigt die Probenstruktur mit modifizierten Wachstumsparametern aus dem Fit, siehe auch
Tabelle 2.2. .
Das Inset zeigt die Probenstruktur mit modifizierten Wachstumsparametern aus dem Fit, siehe auch
Tabelle 2.2.
- Scheinbares Dotierungsprofil der Probe Z14a, errechnet mit
(2.5) aus der gemessenen CV-Kennlinie - siehe Abbildung 2.8. Zwischen
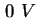 und
und 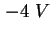 ergibt sich eine Dotierung von ca. ergibt sich eine Dotierung von ca.
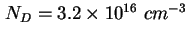 , es folgen die
Quantenpunkte, in deren Umgebung die Störstellen ionisiert sind, und ein Bereich mit einer Dotierung von
ca. , es folgen die
Quantenpunkte, in deren Umgebung die Störstellen ionisiert sind, und ein Bereich mit einer Dotierung von
ca.
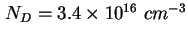 . .
- Berechnete Ladungsträgerdichte in der Probe Z14a bei verschiedenen
Spannungen, die Raumladungszone überstreicht bei steigender Sperrspannung die Quantenpunkte.
- Berechneter Bandkantenverlauf in der Probe Z14a. Für
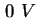 ist der
Verlauf in der ganzen Struktur dargestellt, für ist der
Verlauf in der ganzen Struktur dargestellt, für 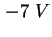 und und 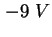 in der Umgebung der Quantenpunkte.
Deutlich zu erkennen ist, wie bei steigender Sperrspannung die Quantenpunkt-Energieniveaus über das
Quasi-Fermi-Niveau in der Umgebung der Quantenpunkte.
Deutlich zu erkennen ist, wie bei steigender Sperrspannung die Quantenpunkt-Energieniveaus über das
Quasi-Fermi-Niveau 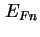 geschoben werden. geschoben werden.
- Experimentelle (Symbol) und errechnete (Rot) CV-Kennlinie der Probe T3189
[Kap99]. Die Rechnung ergibt eine Lage der Energieniveaus bei
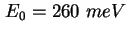 und und
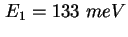 mit Verbreiterungen von
mit Verbreiterungen von
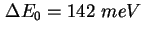 und und
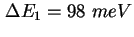 . Das Inset
zeigt die Probenstruktur mit modifizierten Wachstumsparametern aus dem Fit, siehe auch Tabelle
2.4. . Das Inset
zeigt die Probenstruktur mit modifizierten Wachstumsparametern aus dem Fit, siehe auch Tabelle
2.4.
- a) XSTEM-Aufnahme des Dreifach-Stapels Quantenpunkte in Probe T3189,
b) Vergrößerung eines einzelnen Stapels, c) Abmessungen des Stapels aus TEM-Aufnahmen [Kap99],
[Kap01].
- Scheinbares Dotierungsprofil der Probe T3189, errechnet mit
(2.5) aus der gemessenen CV-Kennlinie - siehe Abbildung 2.12. Zwischen
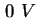 und
und 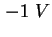 ergibt sich eine Dotierung von ca. ergibt sich eine Dotierung von ca.
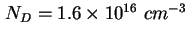 , es folgen die Quantenpunkte,
wobei die zwei Plateaus klar erkennbar sind, und ein Bereich mit einer Dotierung von ca. , es folgen die Quantenpunkte,
wobei die zwei Plateaus klar erkennbar sind, und ein Bereich mit einer Dotierung von ca.
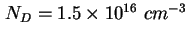 . .
- Experimentelle (Symbol) und errechnete (Rot) CV-Kennlinie der Probe 752-3
[Sch01b]. Die Rechnung ergibt eine Lage der beiden Energieniveaus bei
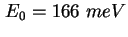 und und
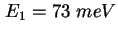 mit Verbreiterungen mit Verbreiterungen
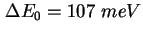 und und
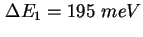 . Das Inset
zeigt die Probenstruktur mit den modifizierten Wachstumsparametern, siehe auch Tabelle 2.6. . Das Inset
zeigt die Probenstruktur mit den modifizierten Wachstumsparametern, siehe auch Tabelle 2.6.
- Scheinbares Dotierungsprofil der Probe 752-3, errechnet mit
(2.5) aus der gemessenen CV-Kennlinie - siehe Abbildung 2.15. Zwischen
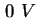 und
und 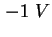 ergibt sich eine Dotierung von ca. ergibt sich eine Dotierung von ca.
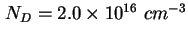 , es folgen die Quantenpunkte
(ein Teil des Kurvenverlaufs liegt hier außerhalb des Plots) und ein Bereich mit einer Dotierung von ca. , es folgen die Quantenpunkte
(ein Teil des Kurvenverlaufs liegt hier außerhalb des Plots) und ein Bereich mit einer Dotierung von ca.
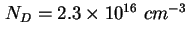 . .
- Experimentelle (Symbol) und errechnete (Rot) CV-Kennlinie der Probe 933 [Sch02b].
Die Rechnung ergibt eine Lage der Energieniveaus von
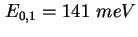 , ,
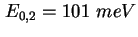 und und
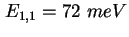 mit Verbreiterungen mit Verbreiterungen
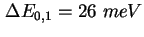 , ,
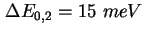 und
und
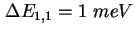 . Das Inset zeigt die Probenstruktur mit den modifizierten
Wachstumsparametern, siehe auch Tabelle 2.8. . Das Inset zeigt die Probenstruktur mit den modifizierten
Wachstumsparametern, siehe auch Tabelle 2.8.
- Leitungsbandkantenverlauf der Probe 933 bei
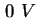 . In der Umgebung
der Quantenpunkte liegt die Bandkante über dem Quasi-Fermi-Niveau, die Störstellen dort sind ionisiert. . In der Umgebung
der Quantenpunkte liegt die Bandkante über dem Quasi-Fermi-Niveau, die Störstellen dort sind ionisiert.
- AFM-Aufnahme von unbedeckten InAs-Quantenpunkten - Probe 931 [Sch02b].
- Scheinbares Dotierungsprofil der Probe 933, errechnet mit
(2.5) aus der gemessenen CV-Kennlinie - siehe Abbildung 2.17. Zwischen
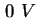 und und 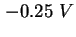 ergibt sich eine Dotierung von ca. ergibt sich eine Dotierung von ca.
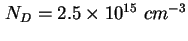 , es folgen
die Quantenpunkte (ein Teil des Kurvenverlaufs liegt hier außerhalb des Plots), man kann deutlich die
beiden Plateaus sehen, und ein Bereich mit einer Dotierung von ca. , es folgen
die Quantenpunkte (ein Teil des Kurvenverlaufs liegt hier außerhalb des Plots), man kann deutlich die
beiden Plateaus sehen, und ein Bereich mit einer Dotierung von ca.
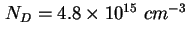 . .
- Experimentelle (Symbol) und errechnete (Rot) CV-Kennlinie der Probe R1137A [Kap00b].
Die Rechnung ergibt eine Tiefe des harmonischen Potentials von
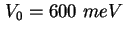 und einem Radius von und einem Radius von
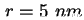 (Abschnitt 2.3.1). Das Inset zeigt die Probenstruktur mit den modifizierten
Wachstumsparametern, siehe auch Tabelle 2.10. (Abschnitt 2.3.1). Das Inset zeigt die Probenstruktur mit den modifizierten
Wachstumsparametern, siehe auch Tabelle 2.10.
- Scheinbares Dotierungsprofil der Probe R1137A errechnet mit
(2.5) aus der gemessenen CV-Kennlinie - siehe Abbildung 2.21. Zwischen
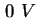 und
und 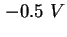 ist keine Dotierung ablesbar (die Ladung in den Quantenpunkten hat die Umgebungsladung
verdrängt), es folgen die Quantenpunkte, ab ist keine Dotierung ablesbar (die Ladung in den Quantenpunkten hat die Umgebungsladung
verdrängt), es folgen die Quantenpunkte, ab 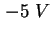 ergibt sich eine Dotierung von ca. ergibt sich eine Dotierung von ca.
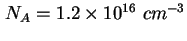 , mit starkem Gradienten. , mit starkem Gradienten.
- Experimentelle (Symbol) und errechnete (Rot) CV-Kennlinie der Probe TU5823 [Gel02].
Die Rechnung ergibt eine Lage der Energieniveaus von
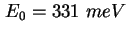 und und
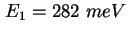 mit Verbreiterungen mit Verbreiterungen
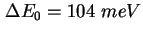 und und
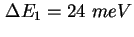 . Das Inset zeigt die Probenstruktur mit
den modifizierten Wachstumsparametern, siehe auch Tabelle 2.11. . Das Inset zeigt die Probenstruktur mit
den modifizierten Wachstumsparametern, siehe auch Tabelle 2.11.
- AFM-Aufnahme von unbedeckten GaSb-Quantenpunkten [MK01].
- Scheinbares Dotierungsprofil der Probe TU5823, errechnet mit
(2.5) aus der gemessenen CV-Kennlinie - siehe Abbildung 2.23. Zwischen
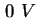 und und 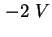 ergibt sich eine Dotierung von ca. ergibt sich eine Dotierung von ca.
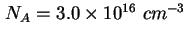 , gefolgt von
einem Gradienten in der Dotierung, den Quantenpunkten, einem Bereich mit einer Dotierung von ca. , gefolgt von
einem Gradienten in der Dotierung, den Quantenpunkten, einem Bereich mit einer Dotierung von ca.
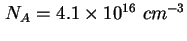 und einem Bereich mit einer Dotierung von ca. und einem Bereich mit einer Dotierung von ca.
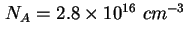 . .
- Schematische Darstellung des Feldeffekttransistors nach G.Yusa und H.Sakaki [Yus97].
Die zugehörige Beschaltung zeigt Abbildung 3.2, den Bandkantenverlauf Abbildung 3.3.
- Hall-Struktur (HFET) zur Messung der Leitfähigkeit
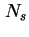 im 2DEG versus der
Gatespannung im 2DEG versus der
Gatespannung 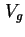 . Eingebettet in das intrinsische GaAs sind die InAs-Quantenpunkte (gelb) [Yus98]. . Eingebettet in das intrinsische GaAs sind die InAs-Quantenpunkte (gelb) [Yus98].
- Skizze des Bandkantenverlaufs in der Struktur. Zwischen der
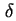 -Dotierung
und dem Schottky-Kontakt wird die Gatespannung -Dotierung
und dem Schottky-Kontakt wird die Gatespannung 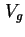 angelegt. Senkrecht zur Zeichenebene dehnt sich das
2DEG (blau) mit zugehöriger Elektronenkonzentration angelegt. Senkrecht zur Zeichenebene dehnt sich das
2DEG (blau) mit zugehöriger Elektronenkonzentration 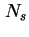 aus. aus.
- Bei
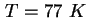 gemessene Hysterese in der
Elektronenkonzentrations-Gatespannungs-Kennlinie [Yus97] ( gemessene Hysterese in der
Elektronenkonzentrations-Gatespannungs-Kennlinie [Yus97] (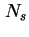 : Elektronendichte im
2DEG-Kanal, : Elektronendichte im
2DEG-Kanal, 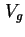 : Gatespannung). : Gatespannung).
- Auger-Prozesse an Quantenpunkten - a) Einfang (Augerrekombination)
b) Emission (Stoßionisation), besetzte Zustände sind schwarz, freie weiß ausgefüllt.
- Phonon-assistierte Prozesse an Quantenpunkten - a) Einfang b) Emission,
besetzte Zustände sind schwarz, freie weiß ausgefüllt.
- Hysterese in der
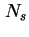 - -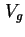 -Kennlinie, modelliert mit der
Augerrekombination als Rekombinationsmechanismus ( -Kennlinie, modelliert mit der
Augerrekombination als Rekombinationsmechanismus (
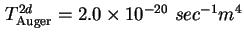 [Usk98]). Deutlich ist der Unterschied zwischen Up-Sweep und Down-Sweep zu sehen. Die rote Kurve
zeigt die stationäre Lösung, also für
[Usk98]). Deutlich ist der Unterschied zwischen Up-Sweep und Down-Sweep zu sehen. Die rote Kurve
zeigt die stationäre Lösung, also für
 . .
- Mittlere Besetzung der Quantenpunkte beim Sweepen, modelliert mit der
Augerrekombination als Rekombinationsmechanismus (
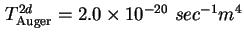 [Usk98]). Ab
[Usk98]). Ab 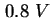 werden die Quantenpunkte beim Up-Sweep besetzt, in diesem Bereich verläuft
die werden die Quantenpunkte beim Up-Sweep besetzt, in diesem Bereich verläuft
die 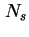 - -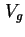 -Kennlinie flach (Abbildung 3.7). Die maximale Besetzung beim Sweepen ist
deutlich geringer als bei der stationären Lösung (rot). -Kennlinie flach (Abbildung 3.7). Die maximale Besetzung beim Sweepen ist
deutlich geringer als bei der stationären Lösung (rot).
- Berechneter Bandkantenverlauf in der Struktur ohne angelegte Spannung
(Punkt (a) in Abbildungen 3.7 und 3.8), das Inset
zeigt zur Orientierung das Bauteil. Die Quantenpunkte sind ungeladen, der Verlauf der Leitungsbandkante
im GaAs ist geradlinig. Im Bereich des 2DEGs liegt die Bandkante unterhalb des Quasi-Fermi-Niveaus.
- Berechneter Bandkantenverlauf in der Struktur mit angelegter Spannung
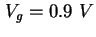 (Punkt (b) in Abbildungen 3.7 und 3.8), das Inset zeigt zur
Orientierung das Bauteil. Das Energieniveau der Quantenpunkte ist unterhalb des Quasi-Fermi-Niveaus,
erstere werden also besetzt. Das 2DEG hat sich ausgedehnt - vergleiche Abbildung 3.9. (Punkt (b) in Abbildungen 3.7 und 3.8), das Inset zeigt zur
Orientierung das Bauteil. Das Energieniveau der Quantenpunkte ist unterhalb des Quasi-Fermi-Niveaus,
erstere werden also besetzt. Das 2DEG hat sich ausgedehnt - vergleiche Abbildung 3.9.
- Berechneter Bandkantenverlauf in der Struktur ohne angelegte Spannung mit
geladenen Quantenpunkten (Punkt (c) in Abbildungen 3.7 und 3.8), das Inset
zeigt zur Orientierung das Bauteil. Aufgrund der Elektronen in den Quantenpunkten hat der Verlauf
der Leitungsbandkante im GaAs einen Knick. Dadurch wird die Bandkante im Bereich des 2DEGs partiell
über das Quasi-Fermi-Niveau verschoben, das 2DEG verkürzt sich - vergleiche Abbildung
3.9
- Hysterese in der
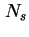 - -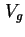 -Kennlinie, einmal modelliert mit dem
Auger-Prozeß und zugehörigem Literaturwert [Usk98] und einmal mit einem Multi-Phononen-Prozeß.
Der zugehörige Koeffizient für den Phonon-assistierten Prozeß wurde durch einen Fit ermittelt. -Kennlinie, einmal modelliert mit dem
Auger-Prozeß und zugehörigem Literaturwert [Usk98] und einmal mit einem Multi-Phononen-Prozeß.
Der zugehörige Koeffizient für den Phonon-assistierten Prozeß wurde durch einen Fit ermittelt.
- Raten an den Quantenpunkten beim Durchfahren der Spannung, einmal modelliert mit
dem Auger-Prozeß und zugehörigem Literaturwert [Usk98] und einmal mit einem Multi-Phononen-Prozeß.
Der zugehörige Koeffizient für den Phonon-assistierten Prozeß wurde durch einen Fit ermittelt. Erst
ab einer Gatespannung von
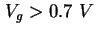 treten nennenswerte Einfangraten auf. Für kleine Spannungen
sind sowohl Einfang als auch Emission sehr gering. treten nennenswerte Einfangraten auf. Für kleine Spannungen
sind sowohl Einfang als auch Emission sehr gering.
- Struktur der Fitroutine mit
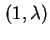 -Evolutionsstrategie [Rec94], [Tür01]. -Evolutionsstrategie [Rec94], [Tür01].
|