Die im vorhergehenden Abschnitt vorgestellten Ergebnisse haben gezeigt, daß die Hysterese in der
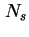 -
-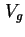 -Kennlinie eines Feldeffekttransistors bestimmt ist durch die Dynamik beim Einfang und bei der
Emission von Ladungsträgern durch die Quantenpunkte. Die Raten sind klein im Vergleich zu der
Sweep-Geschwindigkeit, dadurch werden beim Up-Sweep die Quantenpunkte teilweise besetzt, aufgrund der
geringen Emission bleibt die Besetzung beim Down-Sweep weitestgehend erhalten. Es ergibt sich ein
Unterschied in der Elektronenkonzentration
-Kennlinie eines Feldeffekttransistors bestimmt ist durch die Dynamik beim Einfang und bei der
Emission von Ladungsträgern durch die Quantenpunkte. Die Raten sind klein im Vergleich zu der
Sweep-Geschwindigkeit, dadurch werden beim Up-Sweep die Quantenpunkte teilweise besetzt, aufgrund der
geringen Emission bleibt die Besetzung beim Down-Sweep weitestgehend erhalten. Es ergibt sich ein
Unterschied in der Elektronenkonzentration 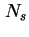 des 2DEGs zwischen Up-Sweep und Down-Sweep (Abbildung
3.7).
des 2DEGs zwischen Up-Sweep und Down-Sweep (Abbildung
3.7).
In den bisherigen Rechnungen wurde davon ausgegangen, daß Einfang und Emission durch den Auger-Prozeß,
siehe Abschnitt 3.2.1, bestimmt sind. Alternativ dazu ist denkbar, daß statt des Auger-Prozesses
die Phonon-assistierten Prozesse, dargestellt in Abschnitt 3.2.2, die Dynamik bestimmen.
Bei experimentellen Untersuchungen des Einfangs- und Emissions-Verhaltens von InAs-Quantenpunkten in
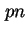 -,
-, 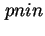 - und
- und 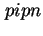 -Dioden wurde eine signifikante Temperaturabhängigkeit der Emission
festgestellt [Hei97], [Kap00a]. Thermische Prozesse haben sich als eine Erklärung für die
Dynamik in den Quantenpunkten im allgemeinen etabliert [Fel01], die Diskussion Auger-Prozeß versus
Phonon-assistierte Prozesse ist kontrovers [Usk97], [Adl96], [Ohn96]. Zu dieser
Diskussion sollen hier anhand eines Vergleichs beider Prozeß-Typen bei der Entstehung der Hysterese
Indizien beigetragen werden.
-Dioden wurde eine signifikante Temperaturabhängigkeit der Emission
festgestellt [Hei97], [Kap00a]. Thermische Prozesse haben sich als eine Erklärung für die
Dynamik in den Quantenpunkten im allgemeinen etabliert [Fel01], die Diskussion Auger-Prozeß versus
Phonon-assistierte Prozesse ist kontrovers [Usk97], [Adl96], [Ohn96]. Zu dieser
Diskussion sollen hier anhand eines Vergleichs beider Prozeß-Typen bei der Entstehung der Hysterese
Indizien beigetragen werden.
Die Ratengleichungen (3.33) beziehungsweise (3.34)
bestimmen die Zahl der Elektronen, die pro Zeiteinheit in die Quantenpunkte hinein oder heraus gehen. In
der Ratengleichung für den Auger-Prozeß (3.33) hängt der Einfang quadratisch
von der Dichte der freien Elektronen über den Quantenpunkten 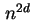 ab. Im Gegensatz dazu hängt
der Einfang bei Phonon-assistierten Prozessen (3.34) nur linear von
ab. Im Gegensatz dazu hängt
der Einfang bei Phonon-assistierten Prozessen (3.34) nur linear von 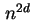 ab. Dieser deutliche Unterschied gibt eine Möglichkeit vor, um beim Einfang der Elektronen einen der
beiden Prozesse als den geeigneteren zu identifizieren.
ab. Dieser deutliche Unterschied gibt eine Möglichkeit vor, um beim Einfang der Elektronen einen der
beiden Prozesse als den geeigneteren zu identifizieren.
Beim Auger-Prozeß liegt ein Literaturwert für den Koeffizienten in der Ratengleichung von
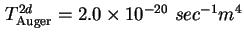 [Usk98] vor. Für Phonon-assistierte Prozesse gibt
es einen Literaturwert für den Koeffizienten des Einphononen-Prozesses, bei dem ein einzelnes Phonon seine
Energie an ein Elektron abgibt beziehungsweise das Gitter von einem Elektron einen Energieanteil in Form
eines Phonons aufnimmt. Ein Phonon in GaAs hat eine Energie von
[Usk98] vor. Für Phonon-assistierte Prozesse gibt
es einen Literaturwert für den Koeffizienten des Einphononen-Prozesses, bei dem ein einzelnes Phonon seine
Energie an ein Elektron abgibt beziehungsweise das Gitter von einem Elektron einen Energieanteil in Form
eines Phonons aufnimmt. Ein Phonon in GaAs hat eine Energie von
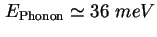 [Ada85].
Das Quantenpunkt-Energieniveau in unserer Rechnung liegt bei
[Ada85].
Das Quantenpunkt-Energieniveau in unserer Rechnung liegt bei
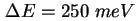 . Um seinen
gebundenen Zustand zu verlassen oder umgekehrt, um von einem Quantenpunkt eingefangen zu werden, ist für
ein Elektron ein Energieaustausch mit sieben Phononen
. Um seinen
gebundenen Zustand zu verlassen oder umgekehrt, um von einem Quantenpunkt eingefangen zu werden, ist für
ein Elektron ein Energieaustausch mit sieben Phononen
 nötig - einem Multi-Phononen-Prozeß. Da ein Literaturwert für den Koeffizienten dieses Multi-Phononen-Prozesses
nicht vorliegt, wurde ein geeignetes
nötig - einem Multi-Phononen-Prozeß. Da ein Literaturwert für den Koeffizienten dieses Multi-Phononen-Prozesses
nicht vorliegt, wurde ein geeignetes
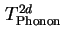 durch Fit an die mittels Auger-Prozeß berechnete
Kurve ermittelt. Für
durch Fit an die mittels Auger-Prozeß berechnete
Kurve ermittelt. Für
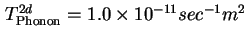 ergibt sich eine sehr gute
Übereinstimmung. Das Ergebnis ist in Abbildung 3.12 dargestellt. Die dazugehörigen Raten
zeigt Abbildung 3.13. Up-Sweep und Down-Sweep sind wieder mit entsprechenden Pfeilen gekennzeichnet.
ergibt sich eine sehr gute
Übereinstimmung. Das Ergebnis ist in Abbildung 3.12 dargestellt. Die dazugehörigen Raten
zeigt Abbildung 3.13. Up-Sweep und Down-Sweep sind wieder mit entsprechenden Pfeilen gekennzeichnet.
Abbildung 3.12:
Hysterese in der 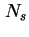 -
-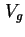 -Kennlinie, einmal modelliert mit dem
Auger-Prozeß und zugehörigem Literaturwert [Usk98] und einmal mit einem Multi-Phononen-Prozeß.
Der zugehörige Koeffizient für den Phonon-assistierten Prozeß wurde durch einen Fit ermittelt.
-Kennlinie, einmal modelliert mit dem
Auger-Prozeß und zugehörigem Literaturwert [Usk98] und einmal mit einem Multi-Phononen-Prozeß.
Der zugehörige Koeffizient für den Phonon-assistierten Prozeß wurde durch einen Fit ermittelt.
![\includegraphics[draft=false, width=11cm]{bilder/hysterese_vgl.eps}](img690.png) |
Für den Einphononen-Prozeß liefert die Literatur einen Wert für den Koeffizienten in der Ratengleichung
von
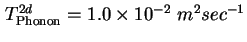 [Fer99]. Das liegt um sieben
Größenordnungen über dem Wert, den ein Fit an die mit dem Auger-Prozeß berechnete Kurve liefert.
Nimmt man als grobe Schätzung an, daß jedes zusätzliche Phonon den Koeffizienten um eine Größenordnung
ändert, so entspricht der gefittete Wert für
[Fer99]. Das liegt um sieben
Größenordnungen über dem Wert, den ein Fit an die mit dem Auger-Prozeß berechnete Kurve liefert.
Nimmt man als grobe Schätzung an, daß jedes zusätzliche Phonon den Koeffizienten um eine Größenordnung
ändert, so entspricht der gefittete Wert für
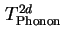 einem Multi-Phononen-Prozeß mit neun Phononen.
Dies deckt sich auch mit der groben Abschätzung aus dem vorhergehenden Absatz, nach der sieben Phononen
benötigt werden, um einem Elektron die
einem Multi-Phononen-Prozeß mit neun Phononen.
Dies deckt sich auch mit der groben Abschätzung aus dem vorhergehenden Absatz, nach der sieben Phononen
benötigt werden, um einem Elektron die 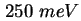 Energie zu geben, die es braucht, um seinen gebundenen
Zustand zu verlassen beziehungsweise umgekehrt, um von einem Quantenpunkt eingefangen zu werden.
Energie zu geben, die es braucht, um seinen gebundenen
Zustand zu verlassen beziehungsweise umgekehrt, um von einem Quantenpunkt eingefangen zu werden.
Praktisch bedeutet das, daß sieben bis neun Phononen gleichzeitig ihre Energie an ein Elektron abgeben
beziehungsweise aufnehmen müssen. Solch ein Multi-Phononen-Prozeß ist als extrem unwahrscheinlich
einzustufen. Man kann die Zahl der zu beteiligenden Phononen argumentativ verringern, da es ausreicht, das
Elektron erst in den angeregten Zustand zu bringen, von wo aus es dann die Quantenpunkte verlassen kann. In
diesem Fall wären zum Beispiel zwei Prozesse mit jeweils vier bis fünf Phononen nötig, wenn angenommen
wird, der angeregte Zustand befinde sich auf halbem Wege zwischen Grundzustand und Leitungsbandkante. Damit
wäre das Problem verlagert, aber nicht gelöst. Es ist gleichermaßen unwahrscheinlich, einen
Multi-Phononen-Prozeß mit sieben bis neun Phononen zu betrachten oder zwei Multi-Phononen-Prozesse mit jeweils vier bis fünf
Phononen, die aber instantan nacheinander auftreten müßten.
Der direkte Vergleich von Auger-Prozeß und Phonon-assistiertem Prozeß zeigt also, daß man mit dem
Auger-Prozeß und zugehörigen Koeffizienten der Ratengleichung aus der Literatur auf Anhieb eine sehr
gute Übereinstimmung mit dem Experiment erzielt. Eine gleich gute Übereinstimmung mit dem Experiment
ergibt sich für Phonon-assistierte Prozesse nur, wenn man einen Multi-Phononen-Prozeß mit sehr
kleiner Rate modelliert.
Den Vergleich mit dem Experiment kann man noch etwas weiter bemühen. Messungen des Einfangs- und
Emissions-Verhaltens von InAs-Quantenpunkten in 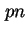 -,
-, 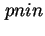 - und
- und 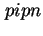 -Dioden zeigen eine starke
Temperaturabhängigkeit von letzterem. Für die Verweildauer der Elektronen in den Quantenpunkten als auch
für deren Relaxationszeiten wurden Werte im Bereich von Pikosekunden bestimmt [Fel01], [Hei97],
[Kap00a], [Ray00].
-Dioden zeigen eine starke
Temperaturabhängigkeit von letzterem. Für die Verweildauer der Elektronen in den Quantenpunkten als auch
für deren Relaxationszeiten wurden Werte im Bereich von Pikosekunden bestimmt [Fel01], [Hei97],
[Kap00a], [Ray00].
Anhand der Ratengleichung (3.33) ergibt sich für den Auger-Prozeß eine
quadratische Abhängigkeit des Einfangs von der Dichte der freien Elektronen über den Quantenpunkten
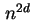 . Für die Emission ist diese Abhängigkeit linear.
Für Phonon-assistierte Prozesse (3.34) ist die Abhängigkeit des Einfangs von
. Für die Emission ist diese Abhängigkeit linear.
Für Phonon-assistierte Prozesse (3.34) ist die Abhängigkeit des Einfangs von
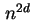 linear, für die Emission hängt sie gar nicht von
linear, für die Emission hängt sie gar nicht von 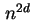 ab.
ab.
Abbildung 3.13:
Raten an den Quantenpunkten beim Durchfahren der Spannung, einmal modelliert mit
dem Auger-Prozeß und zugehörigem Literaturwert [Usk98] und einmal mit einem Multi-Phononen-Prozeß.
Der zugehörige Koeffizient für den Phonon-assistierten Prozeß wurde durch einen Fit ermittelt. Erst
ab einer Gatespannung von
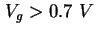 treten nennenswerte Einfangraten auf. Für kleine Spannungen
sind sowohl Einfang als auch Emission sehr gering.
treten nennenswerte Einfangraten auf. Für kleine Spannungen
sind sowohl Einfang als auch Emission sehr gering.
![\includegraphics[draft=false, width=9.7cm]{bilder/raten_vglneu.eps}](img693.png) |
Die Dichte der freien Elektronen über den Quantenpunkten 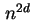 wiederum hängt von der Temperatur
und von der Dotierung des Bauteils ab. Das heißt, für hohe Temperaturen wird der Auger-Prozeß sehr
schnell, sogar noch schneller bei dotierten Strukturen [Usk97]. Für die Multi-Phononen-Prozesse
ist diese Abhängigkeit wesentlich schwächer.
wiederum hängt von der Temperatur
und von der Dotierung des Bauteils ab. Das heißt, für hohe Temperaturen wird der Auger-Prozeß sehr
schnell, sogar noch schneller bei dotierten Strukturen [Usk97]. Für die Multi-Phononen-Prozesse
ist diese Abhängigkeit wesentlich schwächer.
Mit dem Auger-Prozeß kann also sowohl das langsame Einfangs- und Emissionsverhalten bei niedrigen
Temperaturen und geringen Ladungsträgerdichten erklärt werden - so geschehen in diesem Kapitel - als
auch eine mögliche Begründung für die großen Einfangs- und Emissionsraten bei hohen Temperaturen und
Ladungsträgerdichten gegeben werden. Der modellierte Multi-Phononen-Prozeß hingegen würde aufgrund des
kleinen Koeffizienten auch bei hohen Temperaturen und Dichten langsam bleiben.
Damit ist sicherlich keine eindeutige Aussage für einen der beiden Prozesse machbar. Ein Indiz
für den Auger-Prozeß innerhalb der kontroversen Diskussion ist aber gefunden.
![\includegraphics[draft=false, width=11cm]{bilder/hysterese_vgl.eps}](img690.png)
![\includegraphics[draft=false, width=9.7cm]{bilder/raten_vglneu.eps}](img693.png)