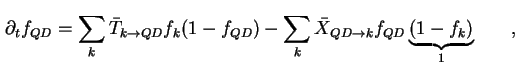|
| (3.19) |
Umgekehrt entnimmt bei der Emission das Elektron dem Gitter die Energie ![]() , um von einem
Quantenpunkt-Energieniveau ins Leitungsband zu gelangen. Es wird also ein unbesetzter Zustand
, um von einem
Quantenpunkt-Energieniveau ins Leitungsband zu gelangen. Es wird also ein unbesetzter Zustand ![]() im
Leitungsband und ein besetzter Zustand
im
Leitungsband und ein besetzter Zustand ![]() in den Quantenpunkten benötigt, daraus folgt
in den Quantenpunkten benötigt, daraus folgt
| (3.20) |
![\includegraphics[draft=false, angle=270, width=12cm]{bilder/phonon_skizze.eps}](img637.png) |
Die zeitliche Änderung der Besetzungswahrscheinlichkeit der Quantenpunkte ist, wenn es sich um
Phonon-assistierte Prozesse handelt, gegeben durch die Summation aller möglichen Phonon-assistierten
Einfänge abzüglich der Summe aller möglichen Phonon-assistierten Emissionen. Jede Wahrscheinlichkeit
wird dabei gewichtet mit
![]() beziehungsweise
beziehungsweise
![]() , den
Koeffizienten für Einfang und Emission (Einheit:
, den
Koeffizienten für Einfang und Emission (Einheit: ![]() ). Es ergibt sich also
). Es ergibt sich also
die Wahrscheinlichkeit, einen unbesetzten Zustand im Leitungsband zu finden, wird wieder gleich eins gesetzt.
Mit der gleichen Argumentation wie im vorhergehenden Abschnitt, läßt sich aus (3.21) eine Differentialgleichung zur Beschreibung der zeitlichen Änderung der Ladungsträgerdichte in den Quantenpunkten ableiten