In dem Modell, das dieser Arbeit zugrunde liegt [Wet98], sind die Grundlagen zur Beschreibung
eines Halbleiterbauelements die eindimensionalen, stationären Strom-Gleichungen (1.15) und die
eindimensionale Poisson-Gleichung (1.10).
Abbildung 1.3:
Selbstkonsistentes Lösungsschema .
![\includegraphics[draft=false, width=9cm, angle=270]{bilder/loesungsschema.epsi}](img192.png) |
In Abbildung 1.3 ist das Vorgehen beim Lösen dieser Gleichungen dargestellt. Dabei
bezeichnen 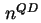 und
und 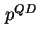 die in den Quantenpunkten lokalisierten Elektronen und Löcher.
Startwerte der Iteration für das Potential
die in den Quantenpunkten lokalisierten Elektronen und Löcher.
Startwerte der Iteration für das Potential 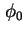 und die Quasi-Fermi-Niveaus
und die Quasi-Fermi-Niveaus 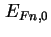 ,
, 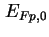 bei angelegter Spannung
bei angelegter Spannung 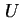 , die die Randbedingungen erfüllen, werden geeignet gewählt - zum Beispiel
ein linearer Verlauf. Als erstes werden daraus mittels der Strom-Gleichungen (1.15) die
Quasi-Fermi-Niveaus
, die die Randbedingungen erfüllen, werden geeignet gewählt - zum Beispiel
ein linearer Verlauf. Als erstes werden daraus mittels der Strom-Gleichungen (1.15) die
Quasi-Fermi-Niveaus
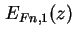 und
und
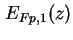 bestimmt. Mit diesen wiederum wird die
Ladungsträgerverteilung
bestimmt. Mit diesen wiederum wird die
Ladungsträgerverteilung
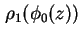 errechnet und daraus mittels der Poisson-Gleichung
(1.10) ein Potential
errechnet und daraus mittels der Poisson-Gleichung
(1.10) ein Potential
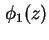 bestimmt. Iterativ wird das wieder zum Berechnen von
bestimmt. Iterativ wird das wieder zum Berechnen von
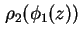 verwendet, woraus wieder ein
verwendet, woraus wieder ein 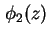 folgt. Diese Schleife wird solange
durchlaufen, bis die Poisson-Gleichung (1.10) hinreichend gelöst ist (Abschnitt
1.5.1). Das Zwischenergebnis
folgt. Diese Schleife wird solange
durchlaufen, bis die Poisson-Gleichung (1.10) hinreichend gelöst ist (Abschnitt
1.5.1). Das Zwischenergebnis
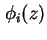 ergibt durch erneutes Lösen der
Strom-Gleichungen (1.15) einen neuen Verlauf der Quasi-Fermi-Niveaus
ergibt durch erneutes Lösen der
Strom-Gleichungen (1.15) einen neuen Verlauf der Quasi-Fermi-Niveaus
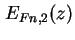 und
und
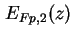 , womit man wiederum die Poisson-Gleichung (1.15) lösen muß. Die Schleifen
werden solange durchlaufen, bis aufeinander folgendes Lösen beider Gleichungen das Potential nicht mehr
verändert.
, womit man wiederum die Poisson-Gleichung (1.15) lösen muß. Die Schleifen
werden solange durchlaufen, bis aufeinander folgendes Lösen beider Gleichungen das Potential nicht mehr
verändert.
![\includegraphics[draft=false, width=9cm, angle=270]{bilder/loesungsschema.epsi}](img192.png)