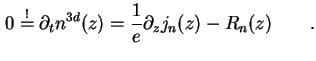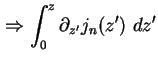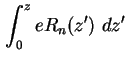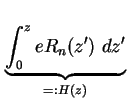|
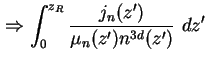 |
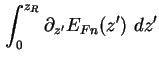 |
(1.51) | |
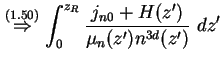 |
(1.52) | ||
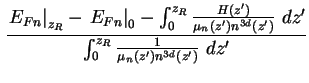 |
(1.53) |
mit dem Ort des rechten Kontakts ![]() .
.
![]() und
und
![]() sind
die Dirichlet-Randbedingungen (1.14) der Strom-Gleichung, die wiederum durch den
Spannungsunterschied
sind
die Dirichlet-Randbedingungen (1.14) der Strom-Gleichung, die wiederum durch den
Spannungsunterschied ![]() gegeben sind.
gegeben sind.
Das Quasi-Fermi-Niveau am Ort z ergibt sich schließlich durch Integration von (1.17) vom
linken Kontakt des Bauteils am Ort ![]() bis z
bis z
| (1.54) | |||
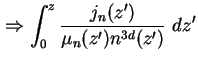 |
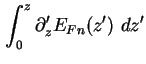 |
(1.55) | |
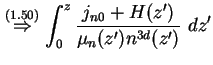 |
(1.56) |
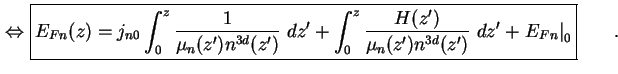 |
(1.57) |
Einsetzen des 1. Moments der Boltzmann-Gleichung (1.17) in das 0. Moment der
Boltzmann-Gleichung (1.15) und zweimaliges Integrieren der resultierenden, inhomogenen
Differentialgleichung zweiter Ordnung in ![]() liefert somit bei gegebenen Randbedingungen das
Quasi-Fermi-Niveau der Ladungsträger.
liefert somit bei gegebenen Randbedingungen das
Quasi-Fermi-Niveau der Ladungsträger.
Für Löcher kann man das Lösungsverfahren analog formulieren, Ausgangspunkt ist dabei die stationäre Strom-Gleichung für Löcher
| (1.58) |