Strom-Gleichungen
Als sogenanntes nulltes Moment der Boltzmann-Gleichung (Herleitung siehe Anhang
A) ergeben sich bei k-unabhängiger Relaxationszeit und parabolischen Bändern
die Strom-Gleichungen (Kontinuitätsgleichungen), hier für Elektronen
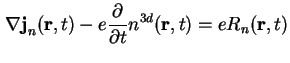 |
(1.12) |
unter Berücksichtigung möglicher Generations-Rekombinations-Prozesse (gr-Prozesse)
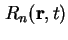 und der Stromdichte der Elektronen
und der Stromdichte der Elektronen
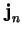 .
.
Wird an ein Bauteil eine Spannung angelegt, so befinden sich die darin enthaltenen Ladungsträger nicht
mehr im Gleichgewicht mit ihrer Umgebung. Für die zwei Sorten von Ladungsträgern (freie Elektronen im
Leitungsband und Donator-Störstellen sowie freie Löcher im Valenzband und Akzeptor-Störstellen)
wird je ein Quasi-Fermi-Niveau 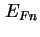 ,
, 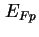 eingeführt, welches das Fermi-Niveau des Gleichgewichts
eingeführt, welches das Fermi-Niveau des Gleichgewichts
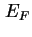 ersetzt (Abschnitt 1.3). Dies erfolgt unter der Annahme, daß auch im Nicht-Gleichgewicht
die Verteilung der besetzten Zustände in jedem Band an jedem Ort einer Fermi-Verteilung gehorcht und
daß die Störstellen im jeweiligen Band im lokalen Gleichgewicht mit den freien Ladungsträgern sind
[Lan91].
ersetzt (Abschnitt 1.3). Dies erfolgt unter der Annahme, daß auch im Nicht-Gleichgewicht
die Verteilung der besetzten Zustände in jedem Band an jedem Ort einer Fermi-Verteilung gehorcht und
daß die Störstellen im jeweiligen Band im lokalen Gleichgewicht mit den freien Ladungsträgern sind
[Lan91].
Das erste Moment der Boltzmann-Gleichung liefert einen Ausdruck für die Stromdichte (Herleitung siehe
Anhang A) in Abhängigkeit vom Quasi-Fermi-Niveau, hier für Elektronen
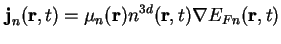 |
(1.13) |
mit der Beweglichkeit der Elektronen 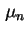 und dem Quasi-Fermi-Niveau der Elektronen
und dem Quasi-Fermi-Niveau der Elektronen 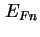 . Ohne
angelegte Spannung liefert (1.13) das räumlich konstante Fermi-Niveau
. Ohne
angelegte Spannung liefert (1.13) das räumlich konstante Fermi-Niveau 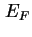 .
.
Einsetzen von (1.13) in (1.12) ergibt eine Differentialgleichung zweiter Ordnung in
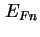 , für die Randbedingungen benötigt werden [Wüs95, Satz 24.7]. Die Stromgleichung bestimmt
in späteren Rechnungen das Quasi-Fermi-Niveau, entsprechend läßt sich als Dirichlet-Randbedingung
(
, für die Randbedingungen benötigt werden [Wüs95, Satz 24.7]. Die Stromgleichung bestimmt
in späteren Rechnungen das Quasi-Fermi-Niveau, entsprechend läßt sich als Dirichlet-Randbedingung
(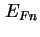 auf
auf
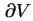 gegeben) formulieren
gegeben) formulieren
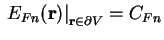 |
(1.14) |
mit der Konstanten 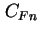 .
.
Wie schon im Abschnitt 1.1 nutzt man die konstanten Struktureigenschaften des Bauteils in
lateraler Richtung aus und daher werden ausschließlich die eindimensionalen Strom-Gleichungen
betrachtet, wodurch der Rechenaufwand wiederum reduziert wird. Es gilt
und
mit der Stromdichte der Löcher 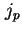 , deren Quasi-Fermi-Niveau
, deren Quasi-Fermi-Niveau 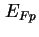 , Beweglichkeit
, Beweglichkeit
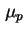 und möglichen gr-Prozessen
und möglichen gr-Prozessen 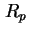 .
.
Zur Lösung der Strom-Gleichungen fehlen jetzt noch Ausdrücke für die Ladungsträgerdichten, die im
folgenden Abschnitt 1.3 abgeleitet werden.