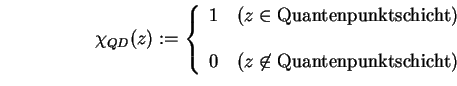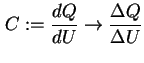Algorithmus

Aus den in Kapitel 1 beschriebenen Grundlagen wird nun ein Programm zusammengestellt, daß die zu untersuchenden Strukturen beschreibt.

Die Simulation ist eindimensional in Wachstumsrichtung (negative z-Achse). Grundlage zur Beschreibung eines Bauteils sind in diesem Modell [Wet98] die eindimensionale Poisson-Gleichung

$$\epsilon_0 \partial_z \lbrack \epsilon( z ) \partial_z \phi ( z ) \rbrack = - \rho ( \phi ( z ) )$$ (2.11)

und, bei Vernachlässigung von Generations-Rekombinations-Prozessen, die eindimensionalen, stationären, homogenen Strom-Gleichungen

$$\partial_z j_n ( z ) = 0 \qquad \land \qquad \partial_z j_p ( z ) = 0 \qquad.$$ (2.12)

Mit der charakteristischen Funktion $\chi_{QD}$, die eins ist bei den Quantenpunkten und null im restlichen Bereich des Bauteils,

$$\chi_{QD} ( z ) := \left\{ \begin{array}{c} 1 \quad (z \in \t... ...\quad (z \not\in \text{Quantenpunktschicht}) \end{array}\right.$$ (2.13)

wird Ladungsträgerdichte (1.7) ergänzt um die Dichte der in den Quantenpunkten gebundenen Elektronen $n^{QD}$ und Löcher $p^{QD}$,

$$\rho ( z ) = - e \lbrack p^{3d}(z) - n^{3d}(z) + N^{+}_{D}(z) - N^{-}_{A}(z) + \chi_{QD} ( z ) p^{QD} - \chi_{QD} ( z ) n^{QD} \rbrack \qquad.$$ (2.14)

Für Ohm'sche Kontakte beziehungsweise Ohm'scher und Schottky-Kontakt werden (2.12) gelöst, um die Quasi-Fermi-Niveaus $E_{Fp}$, $E_{Fn}$ zu bestimmen - siehe auch Kapitel 1.4. Bei Schottky-Dioden ist einer der beiden Ohm'schen Kontakte durch einen Schottky-Kontakt ersetzt worden. Entsprechend ist das Bauteil ausschließlich n- oder p-dotiert.

Die Quasi-Fermi-Niveaus zusammen mit der Annahme, daß die Spannung $U$ zu gleichen Teilen an beiden Kontakten angelegt wird, liefert die Dirichlet-Randbedingung (1.8) für die Poisson-Gleichung. Selbstkonsistentes Lösen von dieser liefert das Potential $\phi(z)$. Mit Quasi-Fermi-Niveaus und Potential zusammen ist das Bauteil eindeutig beschrieben.

Mittels der Definition der Kapazität

$$C := \frac{d Q}{d U} \to \frac{\Delta Q}{\Delta U}$$ (2.15)

läßt sich die CV-Kennlinie bestimmen. Man löst für eine gegebene Spannung $U$ die Poisson-Gleichung (2.11) und die Strom-Gleichungen (2.12) und erhält so über das Potential $\phi$ die Ladung $Q$ im Bauteil. Erhöhen der Spannung $U$, erneutes Lösen von (2.11) und (2.12) liefert die Änderung der Ladung $Q$ mit der Spannung $U$ und damit die Kapazität $C$.

Ein Ausdruck zur Berechnung der Ladung $Q$ im Bauteil in Abhängigkeit von der angelegten Spannung $U$ wird im folgenden Abschnitt hergeleitet.