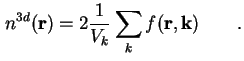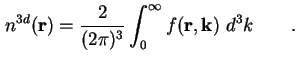|
![$\displaystyle f ( \textbf{r}, \textbf{k} ) = \frac{1}{1+exp( \beta [E ( \textbf{r}, \textbf{k})-E_F])}$](img129.png) |
(1.19) |
mit
![]() und der Boltzmann-Konstanten
und der Boltzmann-Konstanten ![]() . Der Verlauf der Energie
. Der Verlauf der Energie
![]() ist bestimmt durch die Bandstruktur
ist bestimmt durch die Bandstruktur ![]() im
im
![]() -Raum, das Potential
-Raum, das Potential ![]() und den Bandkantenverlauf
und den Bandkantenverlauf
![]() der verwendeten Halbleitermaterialien inklusive der Bandkantensprünge beim abrupten Übergang von
einem Material zu einem anderen (Heterostrukturen).
der verwendeten Halbleitermaterialien inklusive der Bandkantensprünge beim abrupten Übergang von
einem Material zu einem anderen (Heterostrukturen).
| (1.20) |
Für die Bandstruktur
![]() gilt in parabolischer Näherung
gilt in parabolischer Näherung
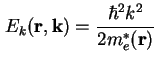 |
(1.21) |
mit der effektiven Masse der Elektronen ![]() und dem Planck'schem Wirkungsquantum
und dem Planck'schem Wirkungsquantum
![]() .
.
Die Zahl der Elektronen im Leitungsband ergibt sich durch Summation über alle besetzten Zustände ![]() innerhalb eines gedachten Volumens
innerhalb eines gedachten Volumens ![]() (zum Beispiel die Brillouin-Zone) unter Berücksichtigung der
Spinentartung, wobei jeder Zustand gewichtet ist mit der entsprechenden Besetzungswahrscheinlichkeit der
Fermi-Dirac-Verteilung
(zum Beispiel die Brillouin-Zone) unter Berücksichtigung der
Spinentartung, wobei jeder Zustand gewichtet ist mit der entsprechenden Besetzungswahrscheinlichkeit der
Fermi-Dirac-Verteilung
Da die Zustände dicht liegen, wird im thermodynamischen Limes (große Volumina) der Übergang zum Quasikontinuum gemacht,
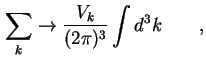 |
(1.23) |
damit formt sich (1.22) um zu
Wird von einer einfachen sphärischen Energieoberfläche ausgegangen, so kann man das Integral in (1.24)
durch Transformation der Integrationsvariablen k überführen in ein Integral über die Energie
![]() . Die Integration erfolgt über die gesamte, positive Energieachse, da wir
von einem parabolischen Band ausgehen, bei dem sich die Zustände im Minimum konzentrieren. Obiges
Integral konvergiert trotz der Annahme eines parabolischen Bandverlaufs, da die Fermi-Verteilung
. Die Integration erfolgt über die gesamte, positive Energieachse, da wir
von einem parabolischen Band ausgehen, bei dem sich die Zustände im Minimum konzentrieren. Obiges
Integral konvergiert trotz der Annahme eines parabolischen Bandverlaufs, da die Fermi-Verteilung
![]() für
für
![]() exponentiell gegen Null geht.
Führt man die effektive Zustandsdichte im Leitungsband
exponentiell gegen Null geht.
Führt man die effektive Zustandsdichte im Leitungsband
![]()
![$\displaystyle N^{3d}_c (\textbf{r}) = 2 \left[ \frac{m_e^* (\textbf{r})}{2 \pi \hbar^2 \beta} \right]^{3/2}$](img150.png) |
(1.25) |
mit der Kreiszahl ![]() ein und definiert mit der Gamma-Funktion
ein und definiert mit der Gamma-Funktion
![]() [Bro81] das
Fermi-Integral der Ordnung
[Bro81] das
Fermi-Integral der Ordnung
![]() (siehe Anhang C)
(siehe Anhang C)
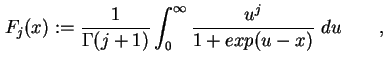 |
(1.26) |
so läßt sich (1.24) mit dem Leitungsbandkantenverlauf
![]() schreiben als
schreiben als
Für die Zahl der besetzten Valenzband-Energieniveaus findet man mit dem Valenzbandkantenverlauf
![]() und der effektiven Zustandsdichte im Valenzband
und der effektiven Zustandsdichte im Valenzband
![]() analog
analog
Beim Anlegen einer Spannung werden Quasi-Fermi-Niveaus eingeführt, welche das Fermi-Niveau des
Gleichgewichts ersetzen (Abschnitt 1.2). Mit dem Quasi-Fermi-Niveau ![]() für Elektronen
und
für Elektronen
und ![]() für Löcher werden die Ausdrücke (1.27) und (1.28) zu
für Löcher werden die Ausdrücke (1.27) und (1.28) zu