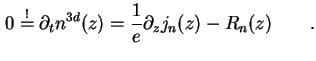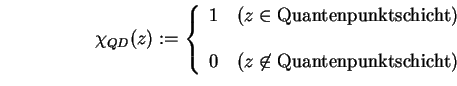Die in Kapitel 1 dargestellten Grundlagen werden jetzt zu einem Programm zusammengesetzt,
das einen Feldeffekttransistor mit Quantenpunkten beschreibt.
Genau wie in Kapitel 2 ist die Simulation eindimensional in Wachstumsrichtung (negative
z-Achse). In dem verwendeten Modell [Wet98] sind die Grundlage zur Beschreibung eines Bauteils
die eindimensionale Poisson-Gleichung
![$\displaystyle \epsilon_0 \partial_z \left[ \epsilon ( z ) \partial_z \phi ( z ) \right] = - \rho ( \phi ( z ) ) \qquad,$](img654.png) |
(3.29) |
und die eindimensionale Strom-Gleichung für Elektronen (das Bauteil ist unipolar)
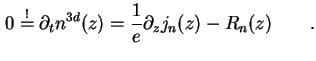 |
(3.30) |
Mit der charakteristischen Funktion 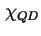 , die eins ist bei den Quantenpunkten und null im
restlichen Bereich des Bauteils,
, die eins ist bei den Quantenpunkten und null im
restlichen Bereich des Bauteils,
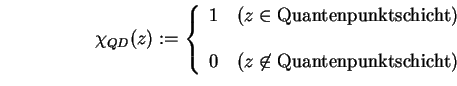 |
|
|
(3.31) |
gilt für die Rate 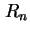
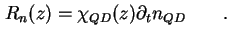 |
(3.32) |
Verwendet werden die entsprechenden Ratengleichungen, für den Auger-Prozeß
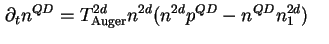 |
(3.33) |
beziehungsweise für Phonon-assistierte Prozesse
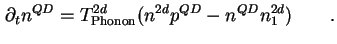 |
(3.34) |
Die Ladungsträgerdichte in (3.29) setzt sich zusammen aus
![$\displaystyle \rho ( z ) = - e [ N_D^+ (z) - n^{3d} ( z ) - \chi_{QD} ( z ) n^{QD} ] \qquad.$](img658.png) |
(3.35) |
Entsprechend der Schaltung in Abbildung 3.2 wird die gesamte Gatespannung 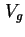 am Schottky-Kontakt
angelegt (siehe auch Kapitel 1). Die dortige Dirichlet-Randbedingung für das Potential
am Schottky-Kontakt
angelegt (siehe auch Kapitel 1). Die dortige Dirichlet-Randbedingung für das Potential
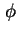 lautet daher
lautet daher
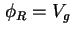 . Bei der
. Bei der 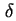 -Dotierung gibt deren Ladung ein Feld vor, die
resultierende Neumann-Randbedingung ist
-Dotierung gibt deren Ladung ein Feld vor, die
resultierende Neumann-Randbedingung ist
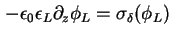 .
Im Bereich des
Al
.
Im Bereich des
Al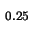 Ga
Ga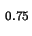 As wird angenommen, daß kein Strom fließt, das
Quasi-Fermi-Niveau
As wird angenommen, daß kein Strom fließt, das
Quasi-Fermi-Niveau 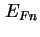 ist hier folglich null. Am Übergang
Al
ist hier folglich null. Am Übergang
Al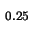 Ga
Ga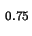 As-GaAs
gilt für
As-GaAs
gilt für 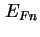 als Dirichlet-Randbedingung
als Dirichlet-Randbedingung
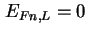 . Am Ort des Schottky-Kontakts ist der
Abstand Leitungsbandkante zum Quasi-Fermi-Niveau durch die Schottky-Barrierenhöhe
. Am Ort des Schottky-Kontakts ist der
Abstand Leitungsbandkante zum Quasi-Fermi-Niveau durch die Schottky-Barrierenhöhe 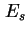 gegeben. Als
Nullpunkt der Energie wird das Valenzband im GaAs gewählt, damit ergibt sich die Lage des Leitungsbandes
durch das Bandgap
gegeben. Als
Nullpunkt der Energie wird das Valenzband im GaAs gewählt, damit ergibt sich die Lage des Leitungsbandes
durch das Bandgap 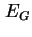 . Die Dirichlet-Randbedingung für das Quasi-Fermi-Niveau am Schottky-Kontakt
lautet bei angelegter Spannung damit
. Die Dirichlet-Randbedingung für das Quasi-Fermi-Niveau am Schottky-Kontakt
lautet bei angelegter Spannung damit
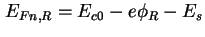 .
.
Selbstkonsistentes Lösen der Poisson-Gleichung (3.29) liefert das Potential 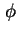 im
Bauteil. Mit
im
Bauteil. Mit 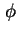 und der daraus resultierenden Elektronendichte
und der daraus resultierenden Elektronendichte 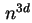 wird die Strom-Gleichung
(3.30) gelöst, das Quasi-Fermi-Niveau der Elektronen
wird die Strom-Gleichung
(3.30) gelöst, das Quasi-Fermi-Niveau der Elektronen 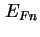 bestimmt. Für
bestimmt. Für 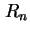 wird dabei der Wert des vorhergehenden Spannungsschritts übernommen beziehungsweise beim allerersten
Rechenschritt wird
wird dabei der Wert des vorhergehenden Spannungsschritts übernommen beziehungsweise beim allerersten
Rechenschritt wird 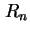 gleich null gesetzt. Mit Potential
gleich null gesetzt. Mit Potential 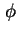 und Quasi-Fermi-Niveau
und Quasi-Fermi-Niveau 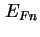 läßt
sich nach (3.33) beziehungsweise (3.34) jetzt eine Rate
läßt
sich nach (3.33) beziehungsweise (3.34) jetzt eine Rate
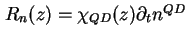 ausrechnen. Es wird erneut die Poisson-Gleichung
(3.29) und die Strom-Gleichung (3.30) unter Berücksichtigung der
Rate
ausrechnen. Es wird erneut die Poisson-Gleichung
(3.29) und die Strom-Gleichung (3.30) unter Berücksichtigung der
Rate 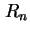 gelöst. Diese Rechenschritte werden wiederholt, bis aufeinander folgendes Lösen von
(3.29), (3.30) und (3.33) beziehungsweise
(3.34) das Ergebnis nicht mehr verändert. Die Ladungsträgerdichte
gelöst. Diese Rechenschritte werden wiederholt, bis aufeinander folgendes Lösen von
(3.29), (3.30) und (3.33) beziehungsweise
(3.34) das Ergebnis nicht mehr verändert. Die Ladungsträgerdichte 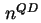 in den
Quantenpunkten wird dabei nicht mitvariiert.
in den
Quantenpunkten wird dabei nicht mitvariiert.
Die Rate 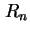 aus der zu einer angelegten Gatespannung
aus der zu einer angelegten Gatespannung 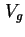 konvergierten Lösung bestimmt den Zeitschritt
konvergierten Lösung bestimmt den Zeitschritt
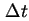 . Pro Schritt soll sich die Ladung in den Quantenpunkten maximal um einen vorzugebenden
Wert
. Pro Schritt soll sich die Ladung in den Quantenpunkten maximal um einen vorzugebenden
Wert
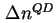 ändern. Aus den Experimenten ist eine Sweep-Zeit von ,,mehreren Sekunden``
bekannt [Yus97], woraus man auf eine ungefähre Sweep-Geschwindigkeit zurückschließen kann. Die
Spannungsachse wird zerlegt in Teilintervalle
ändern. Aus den Experimenten ist eine Sweep-Zeit von ,,mehreren Sekunden``
bekannt [Yus97], woraus man auf eine ungefähre Sweep-Geschwindigkeit zurückschließen kann. Die
Spannungsachse wird zerlegt in Teilintervalle
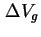 , zu jedem Teilintervall ergibt sich aus
der Sweep-Geschwindigkeit eine Verweildauer
, zu jedem Teilintervall ergibt sich aus
der Sweep-Geschwindigkeit eine Verweildauer
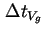 .
.
Bei positivem Vorzeichen der Rate 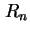 werden die Quantenpunkte mit Elektronen besetzt. Aus der Rate und
werden die Quantenpunkte mit Elektronen besetzt. Aus der Rate und
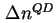 wird ein Zeitschritt
wird ein Zeitschritt 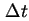 errechnet. Es muß dabei zwischen zwei
Möglichkeiten unterschieden werden:
errechnet. Es muß dabei zwischen zwei
Möglichkeiten unterschieden werden:
- der Zeitschritt
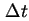 beziehungsweise die Summe aller Zeitschritte dieses Spannungsintervalls sind kleiner
als die Verweildauer
beziehungsweise die Summe aller Zeitschritte dieses Spannungsintervalls sind kleiner
als die Verweildauer
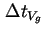 , dann wird die Ladung in den Quantenpunkten
, dann wird die Ladung in den Quantenpunkten 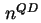 erhöht
gemäß
erhöht
gemäß
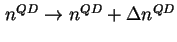 , die neue Systemzeit
, die neue Systemzeit 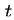 ergibt sich aus
ergibt sich aus
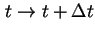 ; mit dem neuen
; mit dem neuen 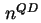 werden wieder
(3.29) und (3.30) gelöst, der nächste Zeitschritt folgt
werden wieder
(3.29) und (3.30) gelöst, der nächste Zeitschritt folgt
- der Zeitschritt
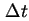 beziehungsweise die Summe aller Zeitschritte dieses Spannungsintervalls sind größer
als die Verweildauer
beziehungsweise die Summe aller Zeitschritte dieses Spannungsintervalls sind größer
als die Verweildauer
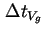 , dann wird die Ladung in den Quantenpunkten
, dann wird die Ladung in den Quantenpunkten 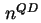 erhöht um
den Anteil von
erhöht um
den Anteil von
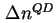 , der der Differenz aus aktuellem Zeitschritt
, der der Differenz aus aktuellem Zeitschritt 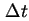 beziehungsweise der Summe aller Zeitschritte dieses Spannungsintervalls und der Verweildauer
beziehungsweise der Summe aller Zeitschritte dieses Spannungsintervalls und der Verweildauer
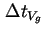 entspricht; die Systemzeit
entspricht; die Systemzeit 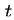 wird auf das Ende des Intervalls
wird auf das Ende des Intervalls
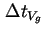 gesetzt, mit dem neuen
gesetzt, mit dem neuen 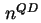 und dem nächsten Spannungsintervall
und dem nächsten Spannungsintervall
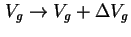 werden wieder (3.29) und (3.30) für den nächsten Zeitschritt gelöst.
werden wieder (3.29) und (3.30) für den nächsten Zeitschritt gelöst.
Bei negativem Vorzeichen der Rate 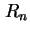 verlassen die Elektronen die Quantenpunkte. Das Vorgehen ist
identisch zum eben skizzierten, nur wird die Ladung
verlassen die Elektronen die Quantenpunkte. Das Vorgehen ist
identisch zum eben skizzierten, nur wird die Ladung 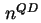 in den Quantenpunkten erniedrigt und nicht
erhöht.
in den Quantenpunkten erniedrigt und nicht
erhöht.
Um die Kennlinie zu erhalten, startet man bei 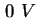 und
und
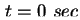 . Da man davon ausgehen kann, daß
vor der Messung das Bauteil beliebig lange Zeit hat, um ins Gleichgewicht zu gelangen, ergibt sich die
initiale Besetzung der Quantenpunkte aus der Ratengleichung mittels (3.33)
und (3.34) nach
. Da man davon ausgehen kann, daß
vor der Messung das Bauteil beliebig lange Zeit hat, um ins Gleichgewicht zu gelangen, ergibt sich die
initiale Besetzung der Quantenpunkte aus der Ratengleichung mittels (3.33)
und (3.34) nach
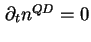 (die initiale Besetzung ist bei beiden
Prozessen gleich). Die Gatespannung wird nach dem vorgestellten Rechenweg durchgefahren bis zu einem
Maximalwert, dann dreht sich das Vorzeichen der Spannungsänderung um. Die Spannung wird in
entgegengesetzter Richtung hin zu ihrem Ausgangspunkt durchgefahren. Integration der Elektronendichte
über den Bereich der z-Achse, wo sich das 2DEG erstreckt, liefert zu jeder Gatespannung
(die initiale Besetzung ist bei beiden
Prozessen gleich). Die Gatespannung wird nach dem vorgestellten Rechenweg durchgefahren bis zu einem
Maximalwert, dann dreht sich das Vorzeichen der Spannungsänderung um. Die Spannung wird in
entgegengesetzter Richtung hin zu ihrem Ausgangspunkt durchgefahren. Integration der Elektronendichte
über den Bereich der z-Achse, wo sich das 2DEG erstreckt, liefert zu jeder Gatespannung 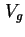 die
Elektronenkonzentration
die
Elektronenkonzentration 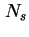 im zweidimensionalen Elektronengas.
im zweidimensionalen Elektronengas.