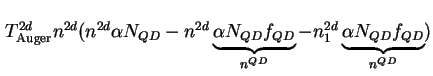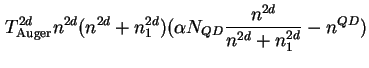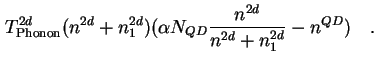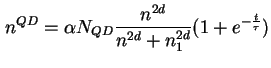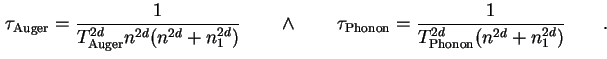Zeitliche Entwicklung

Aus (3.18) beziehungsweise (3.22) läßt sich bei gegebenen Dichten $n^{2d}, n_1^{2d}$ die Rate $\partial_t n^{QD}$ bestimmen und damit ein analytischer Ausdruck für die Emission. Hierzu wird Gleichung (3.17) umgeschrieben

$$\partial_t n^{QD} = T_{\text{Auger}}^{2d} n^{2d} ( n^{2d} \alpha N_{QD} - n^{2d} \und... ...N_{QD} f_{QD}}_{n^{QD}} - n_1^{2d} \underbrace{\alpha N_{QD} f_{QD}}_{n^{QD}} )$$ (3.23)

$$= T_{\text{Auger}}^{2d} n^{2d} ( n^{2d} \alpha N_{QD} - n^{QD} ( n^{2d} + n_1^{2d} ) )$$ (3.24)

$$= T_{\text{Auger}}^{2d} n^{2d} ( n^{2d} + n_1^{2d} ) ( \alpha N_{QD} \frac{n^{2d}}{n^{2d} + n_1^{2d}} - n^{QD} )$$ (3.25) beziehungsweise

$$= T_{\text{Phonon}}^{2d} ( n^{2d} + n_1^{2d} ) ( \alpha N_{QD} \frac{n^{2d}}{n^{2d} + n_1^{2d}} - n^{QD} )\quad.$$ (3.26)

Eine spezielle Lösung von (3.25), die für $t \to \infty$ den stationären Zustand beschreibt, ist also für beide Prozesse bei konstantem $n^{2d}$ stets

$$n^{QD} = \alpha N_{QD} \frac{n^{2d}}{n^{2d} + n_1^{2d}} ( 1 + e^{- \frac{t}{\tau}} )$$ (3.27)

mit

$$\tau_{\text{Auger}} = \frac{1}{T_{\text{Auger}}^{2d}n^{2d}(n^{2d}... ...tau_{\text{Phonon}} = \frac{1}{T_{\text{Phonon}}^{2d}(n^{2d}+n_1^{2d})} \qquad.$$ (3.28)

Zur Befriedigung beliebiger Anfangsbedingungen muß noch eine Lösung der homogenen Differentialgleichung (3.25) beziehungsweise (3.26) addiert werden. Bei der Modellierung wird die Zeitachse in disjunkte Intervalle zerlegt, auf denen $n^{2d}$ als konstant angenommen werden kann.