Diskussion

In diesem Kapitel wurden Kapazitäts-Spannungs-Kennlinien von Quantenpunkten in Halbleiterstrukturen analysiert. Zur Verfügung standen Messungen an unterschiedlichen Bauteilen (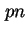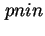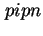$pn$-, $pnin$-, $pipn$- sowie Schottky-Dioden) mit unterschiedlichen Materialsystemen (InAs in GaAs, Ge in Silizium und GaSb in GaAs). Sowohl die Ergebnisse der Bestimmung der elektronischen Struktur der Quantenpunkte aus diesen Fits als auch das notwendige Modifizieren der Wachstumsparameter sind ausführlich diskutiert worden.

Dabei hat sich gezeigt, daß anhand der CV-Messungen nicht nur mittels einfacher Abschätzungen die Dotierungskonzentrationen im Bauteil bestimmbar sind, sondern daß man auch Rückschlüsse auf die elektronische Struktur eingebetteter Quantenpunkten machen kann. Mit Hilfe eines eindimensionalen Modells [Wet98] ist es möglich, den Verlauf der CV-Kennlinien nachzuvollziehen und durch einen Fit an das Experiment die Energieniveaus der in den Quantenpunkten lokalisierten Ladungsträger zu bestimmen. Im Gegensatz zu optischen Methoden, wo Anregungsenergien gemessen werden, also der Abstand zwischen den Energieniveaus von Elektronen und Löchern, kann so mittels der Kapazitäts-Spannungs-Messung die Lage der Energieniveaus in den Quantenpunkten relativ zur Bandkante bestimmt werden.

Für Strukturen beziehungsweise Materialsysteme, wo die Zahl der in den Quantenpunkten gebundenen Ladungsträgern klein ist (InAs in GaAs, 4-8 Elektronen), ergeben sich für das zweifach entartete Grundzustandsniveau Zahlenwerte, die sich gut mit Messungen und k.p-Rechnungen decken. Der Einfluß der Coulomb-Abstoßung liegt hier im Bereich von 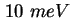$10\ meV$, das heißt bei einer geringen Anzahl von Ladungsträgern ist dieser Einfluß abschätzbar im Vergleich zu den Zahlenwerten für die Lage des Grundzustands. Im angeregten Zustand befinden sich in der Regel mehr Elektronen (4-6), der Einfluß der Coulomb-Abstoßung ist größer. Daher lassen sich die so ermittelten Positionen für den angeregten Zustand aufgrund unseres vereinfachten Modells, wo die Quantenpunkte als homogen geladene Schicht in die Poisson-Gleichung eingehen und damit inter- und intra-dot Wechselwirkungen vernachlässigt werden, schwer diskutieren. An Rechnungen mit einem detaillierteren, dreidimensionalen Modell wird gearbeitet [Wet03].

Eine Stärke dieser Analysen ist, daß mit den genauen Ladungsträgerdichten gearbeitet wird. Effekte, die mit der Umgebung der Quantenpunkte zu tun haben, können so berücksichtigt werden. Bei der Probe 933 (Abschnitt 2.6.4) war es deshalb möglich, die flache Lage der Energieniveaus auf die starke Ausdehnung der Raumladungszone bei 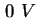$0\ V$ Sperrspannung zurückzuführen. Mit Hilfe des detaillierteren, dreidimensionalen Modells sind daher sehr präzise Aussagen über die elektronische Struktur der Quantenpunkte, eingebettet in eine dotierte Umgebung, zu erwarten.

Bei Materialsystemen, wo in den Quantenpunkten sehr viele Ladungsträger gebunden sind (Ge in Silizium, 50 Löcher; GaSb in GaSb, 15 Löcher), wird der Einfluß der Coulomb-Abstoßung sehr groß, die Ergebnisse des Fits sind physikalisch schwer oder gar nicht mehr interpretierbar.

Bis auf eine Probe (933) wiesen alle Messungen einen konstanten Unterschied (Offset) zwischen gemessener und berechneter Kennlinie von 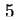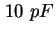$5$-$10\ pF$ auf. Bei der experimentellen Bestimmung der CV-Kennlinie erfolgt eine Kalibrierung so, daß parasitäre Kapazitäten vom Meßplatz aufgrund der verwendeten Kabel etc. von der Messung abgezogen werden. Diese Korrektur entspricht einem positiven oder negativen Offset. Anscheinend kommt es dabei zu einer Verschiebung der Kennlinie, den die Rechnung natürlich nicht wiedergeben kann. Bei der Probe 752-3 (Abschnitt 2.6.3) war die Abweichung allerdings so groß, daß ein Unterschied zwischen modifizierten Wachstumsparametern und scheinbarem Dotierungsprofil darauf zurückzuführen ist.

Zusammenfassend läßt sich feststellen, daß die Kapazitäts-Spannungs-Spektroskopie an Halbleiterstrukturen mit eingebauten Quantenpunkten eine geeignete Methode ist, um die Eigenschaften der Quantenpunkte experimentell zu untersuchen und anschließend mittels Rechnung auszuwerten. Es hat sich dabei als notwendig herausgestellt, sowohl die dreidimensionale Struktur der Quantenpunkte als auch unter Verwendung eines detaillierten Modells die Wechselwirkung der lokalisierten Ladungsträger untereinander zu berücksichtigen. Ferner bietet es sich für zukünftige Rechnungen an, erst die Dotierungen um die Quantenpunkte herum anhand des scheinbaren Dotierungsprofils zu bestimmen und dann mittels Fit die restlichen Parameter (Lage der Energieniveaus etc.) zu ermitteln.