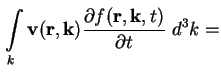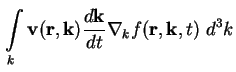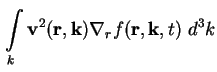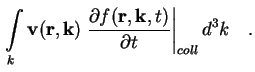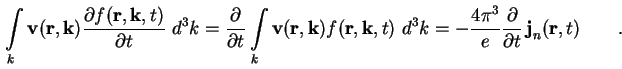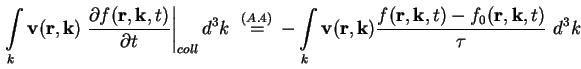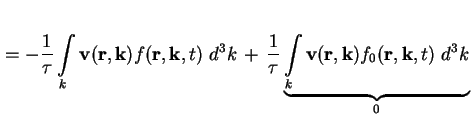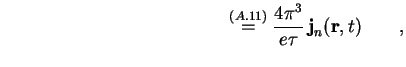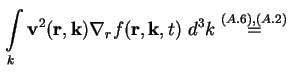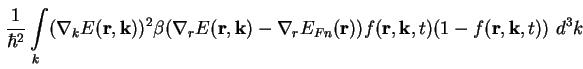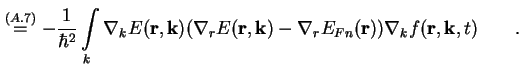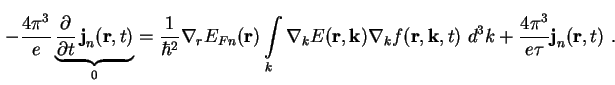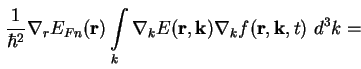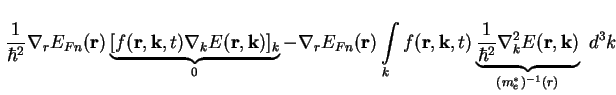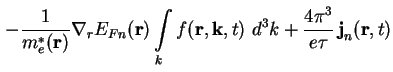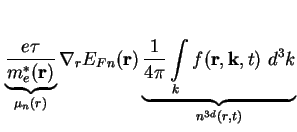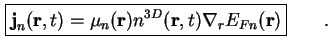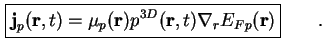1. Moment der Boltzmann-Gleichung

Die Bestimmung des 1. Moments der Boltzmann-Gleichung (A.1) erfolgt durch Multiplikation mit $\textbf{v} ( \textbf{r} , \textbf{k} )$ und Integration über den k-Raum [Sch98], [Sch01a]

$$\int\limits_k \textbf{v} ( \textbf{r} , \textbf{k} ) \frac{\partial f ( \textbf{r}, \textbf{k}, t )}{\partial t} \ d^3 k = - \int\limits_k \textbf{v}(\textbf{r} , \textbf{k} ) \frac{d \textbf{k}}{d t} \nabla_k f ( \textbf{r}, \textbf{k}, t ) \ d^3 k$$

$$- \int\limits_k \textbf{v}^2(\textbf{r} , \textbf{k} ) \nabla_r f ( \textbf{r}, \textbf{k}, t ) \ d^3 k$$

$$+ \int\limits_k \textbf{v}(\textbf{r} , \textbf{k} ) \left. \frac{\... ... f ( \textbf{r}, \textbf{k}, t )}{\partial t} \right\vert _{coll} d^3 k \quad .$$ (A.15)

Die linke Seite von (A.16) läßt sich mit Hilfe der Definition der Stromdichte für Elektronen (A.11) umschreiben zu

$$\int\limits_k \textbf{v} ( \textbf{r} , \textbf{k} ) \frac{\parti... ...pi^3}{e} \frac{\partial}{\partial t} \, \textbf{j}_n ( \textbf{r}, t ) \qquad .$$ (A.16)

Das Integral über den Kollisions-Term in (A.16) formt sich durch Verwenden von (A.4) und (A.11) zu folgendem Ausdruck um

$$\int\limits_k \textbf{v}(\textbf{r} ,... ...textbf{r}, \textbf{k}, t ) - f_{0} ( \textbf{r}, \textbf{k}, t )}{\tau} \ d^3 k$$

$$= -\frac{1}{\tau}\int\limits_k \textbf{v} ( \textbf{r} , \textbf{... ...v} ( \textbf{r} , \textbf{k} ) f_{0} ( \textbf{r}, \textbf{k}, t ) \ d^3 k}_{0}$$

$$\qquad \qquad \qquad \qquad \qquad \q... ...mdichte})}{=} \frac{4 \pi^3}{e \tau} \, \textbf{j}_n ( \textbf{r}, t ) \qquad ,$$ (A.17)

da $f_{0} ( \textbf{r}, \textbf{k}, t )$ die Gleichgewichtsverteilung ist, die mittlere Bewegung ergibt sich dadurch zu null.

Das zweite Integral auf der rechten Seite von (A.16) läßt sich durch Einsetzen von (A.6) und (A.2) schreiben als

$$- \int\limits_k \textbf{v}^2(\textbf{r}... ... \textbf{k}, t ) \ d^3 k \overset{(\ref{FermiAbleitR}), (\ref{BlochGeschw})}{=}$$

$$- \frac{1}{\hbar^2} \int\limits_k ( \nabla_k E ( \textbf{r} , \text... ...f ( \textbf{r}, \textbf{k}, t ) ( 1 - f ( \textbf{r}, \textbf{k}, t ) ) \ d^3 k$$

$$\overset{(\ref{FermiAbleitK})}{=} - \... ... ( \textbf{r} )) \nabla_k f ( \textbf{r}, \textbf{k}, t ) \qquad . \qquad \quad$$ (A.18)

Durch Klammern auflösen in (A.19) und zusammenfassen mit dem ersten Integral auf der rechten Seite von (A.16) (verwende (A.2) und (A.3), Terme addieren sich dann zu Null) ergibt sich im stationären Fall für (A.16) insgesamt

$$- \frac{4 \pi^3}{e} \underbrace{\frac{\partial}{\partial t} \, \t... ...tbf{k}, t ) \ d^3 k + \frac{4 \pi^3}{e \tau} \textbf{j}_n ( \textbf{r}, t ) \ .$$ (A.19)

Das verbleibende Integral in (A.20) wird partiell integriert, die Fermi-Verteilung verschwindet wieder am Rand der Brillouin-Zone und mit der effektiven Masse der Elektronen $m^*_e ( \textbf{r} )$ ergibt sich so

$$\frac{1}{\hbar^2} \nabla_r E_{Fn} ( \textbf{r} ) \int\limits_k \n... ...}, \textbf{k}, t ) \ d^3 k = \qquad \qquad \qquad \qquad \qquad \qquad \quad \,$$

$$\frac{1}{\hbar^2} \nabla_r E_{Fn} ( \textbf{r} ) \underbrace{\lbr... ...\hbar^2} \nabla_k^2 E ( \textbf{r} , \textbf{k} )}_{(m^*_e)^{-1} ( r )} \ d^3 k$$

und damit schlußendlich für (A.16)

$$= - \frac{1}{m^*_e ( \textbf{r} )} \nabla_r E_{Fn} ( \textbf{r} ) \... ...xtbf{k}, t ) \ d^3 k + \frac{4 \pi^3}{e \tau} \, \textbf{j}_n ( \textbf{r}, t )$$ 0

$$\Leftrightarrow \quad \textbf{j}_n ( \textbf{r}, t ) = \underbrace{\frac{e \tau }{m^*_e ( \textbf{r} )}}_{\mu_n (r)} \na... ...\pi} \int\limits_k f ( \textbf{r}, \textbf{k}, t ) \ d^3 k}_{n^{3d} ( r , t ) }$$ (A.20)

mit der Beweglichkeit der Elektronen $\mu_n (\textbf{r})$.

Das 1. Moment der Boltzmann-Gleichung für Elektronen im stationären Fall liefert einen Ausdruck für die Stromdichte

$$\boxed{ \textbf{j}_n ( \textbf{r}, t ) = \mu_n (\textbf{r}) n^{3D} ( \textbf{r} , t ) \nabla_r E_{Fn} ( \textbf{r} ) }\qquad.$$ (A.21)

Für Löcher findet man mit deren Beweglichkeit $\mu_p (\textbf{r})$ analog

$$\boxed{ \textbf{j}_p ( \textbf{r}, t ) = \mu_p (\textbf{r}) p^{3D} ( \textbf{r} , t ) \nabla_r E_{Fp} ( \textbf{r} ) }\qquad.$$ (A.22)