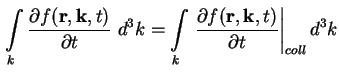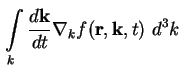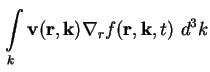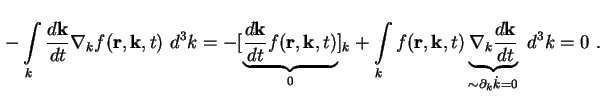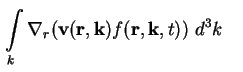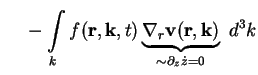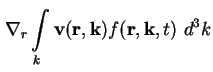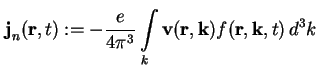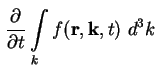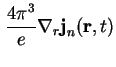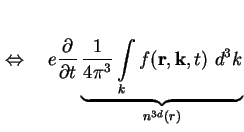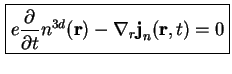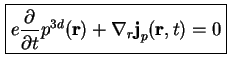0. Moment der Boltzmann-Gleichung

Die Bestimmung des 0. Moments der Boltzmann-Gleichung (A.1) erfolgt durch Integration über den k-Raum [Sch98], [Sch01a]

$$\int\limits_k \frac{\partial f ( \textbf{r}, \textbf{k}, t )}{\pa... ...\partial f ( \textbf{r}, \textbf{k}, t )}{\partial t} \right\vert _{coll} d^3 k - \int\limits_k \frac{d \textbf{k}}{d t} \nabla_k f ( \textbf{r}, \textbf{k}, t ) \ d^3 k$$

$$- \int\limits_k \textbf{v}(\textbf{r} , \textbf{k} ) \nabla_r f ( \textbf{r}, \textbf{k}, t ) \ d^3 k$$

Zuerst betrachten wir die rechte Seite von (A.8). Der Kollisions-Term kann bei kleinen Störungen vernachlässigt werden. Berücksichtigt man, daß $f ( \textbf{r}, \textbf{k}, t )$ am Rand des k-Raums (Brillouin-Zone) verschwindet, läßt sich der zweite Summand des Integrationskerns durch partielles Integrieren über k schreiben als

$$-\int\limits_k \frac{d \textbf{k}}{d t} \nabla_k f( \textbf{r} , ... ...nabla_k \frac{d \textbf{k}}{d t}}_{\sim \partial_k \dot{k} = 0} \ d^3 k = 0 \ .$$ (A.8)

Mit analoger Argumentation schreibt man den dritten Summanden des Integrationskerns von (A.8) unter Verwendung der Produktregel des Differenzierens um

$$\int\limits_k \textbf{v}(\textbf{r} , \textbf{k} ) \nabla_r f ( \textbf{r}, \textbf{k}, t ) \ d^3 k = \int\limits_k \nabla_r ( \textbf{v}(\textbf{r} , \textbf{k} ) f ( \textbf{r}, \textbf{k}, t )) \ d^3 k \quad$$

$${} \quad - \int\limits_k f ( \textbf{r}, \textbf{k}, t ) \underbr... ...a_r \textbf{v}(\textbf{r} , \textbf{k} )}_{\sim \partial_z \dot{z} = 0} \ d^3 k$$

$$= \nabla_r \int\limits_k \textbf{v}(\textbf{r} , \textbf{k} ) f ( \textbf{r}, \textbf{k}, t ) \ d^3 k$$ (A.9)

$${}( ) \qquad.$$

Über die Definition einer Stromdichte für Elektronen $\textbf{j}_n ( \textbf{r}, t )$

$$\textbf{j}_n ( \textbf{r}, t ) : = - \frac{e}{4 \pi^3} \int\limit... ...\textbf{v} ( \textbf{r} , \textbf{k} ) f ( \textbf{r}, \textbf{k}, t ) \, d^3 k$$ (A.10)

läßt sich (A.8) insgesamt schreiben als

$$\frac{\partial}{\partial t} \int\limits_k f ( \textbf{r}, \textbf{k}, t ) \ d^3 k = \frac{4 \pi^3}{e} \nabla_r \textbf{j}_n ( \textbf{r}, t )$$ (A.11)

$$\Leftrightarrow \quad e \frac{\partial}{\partial t} \underbrace{\... ...4 \pi^3} \int\limits_k f ( \textbf{r}, \textbf{k}, t ) \ d^3 k}_{n^{3d} ( r ) } = \nabla_r \textbf{j}_n ( \textbf{r}, t ) \qquad.$$ (A.12)

Gleichung (A.13) ist das sogenannte 0. Moment der Boltzmann-Gleichung, welches hier eine Dynamik beschreibt

$$\boxed{ e \frac{\partial}{\partial t} n^{3d} ( \textbf{r} ) - \nabla_r \textbf{j}_n ( \textbf{r}, t ) = 0 }$$ (A.13)

wobei $n^{3d} ( \textbf{r} )$ die dreidimensionale Elektronendichte ist.

Für Löcher findet man analog

$$\boxed{ e \frac{\partial}{\partial t} p^{3d} ( \textbf{r} ) + \nabla_r \textbf{j}_p ( \textbf{r}, t ) = 0 }$$ (A.14)

mit der Stromdichte der Löcher $\textbf{j}_p$ und der dreidimensionalen Lochdichte $p^{3d}$.