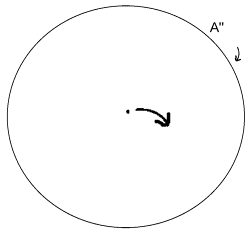
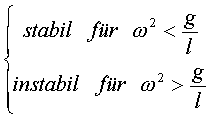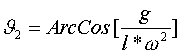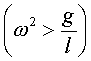4. Beispiele

 

Zentrifugalrotator:

 

 

 

Bewegungsgleichung in Kugelkoordinaten:

 

 

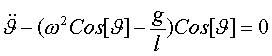
stationäre Lösungen:

 

      

       

 

 

 

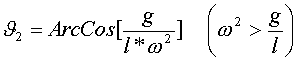
Stabilität:

  

 

     stabil, existiert nur für

 

 

     instabil

 

 

 

 

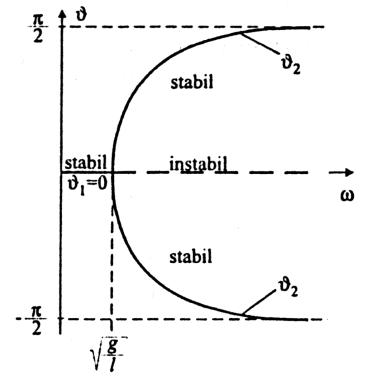
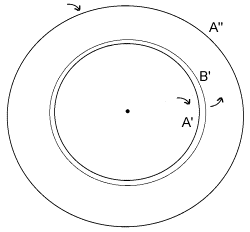
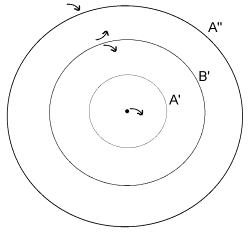
Aus dem Bild im Parameterraum ist ersichtlich, daß es sich um eine Heugabel-Bifurkation handelt (siehe auch Abschnitt 3.3, Beispiel aus "Klassische Mechanik", F.Kuypers, 5. Auflage, VCH-Verlag 1997).


Tacoma Bridge:

 

1. Juli 1940, Tacoma Narrows Bridge, USA

 

 

Windstärken zwischen 65 und 75 km/h regen die Brücke zu Torsionsschwingungen an. Der Sturm verliert nicht an Heftigkeit,  die durch den Wind angeregte Schwingung kommt in Resonanz mit der Eigenfrequenz der Brücke. Die rasch anwachsende Amplitude der Schwingung zerstört am Ende die Tacoma Bridge.

Die Tacoma Bridge ist ein Beispiel für die Cyclic Fold Bifurkation (Sattel-Knoten-Bifurkation eines stabilen und eines instabilen Grenzzyklus):


 

 

 

                                                             

 

A’,A’’: stabiler Grenzzykuls   B: instabiler Grenzzykuls

 

In den obigen Abbildungen kann der Vorgang dieser Bifurkation beobachtet werden. Dabei ist der veränderte Parameter v die Windgeschwindigkeit, die um 2eps zunimmt und so die Auslenkung der Brücke (entspricht dem kleinsten stabilen Zyklus) von A' nach A'' verändert. Für eine so starke Auslenkung war die Brücke jedoch nicht elastisch genug gebaut. Bei der Windgeschwindigkeit vcrit passiert die Bifurkation.

Dabei ist der stabile Grenzzyklus A' mit dem instabilen Grenzzyklus B' kollidiert und beide sind verschwunden; nur der zweite stabile Zyklus A'' ist übergeblieben. Diesen hat die Brücke allerdings nicht überlebt. Die Veränderung des Zyklus von A' auf A'' nennt man auch "Catastrophic Transition". Bei dieser Art der "Catastrophic Bifurcation" handelt es sich um die Cyclic Fold oder auch Periodic Fold Bifurcation, die das Analogon zur Sattel-Knoten-Bifurkation von Fixpunkten (bezüglich des Radius) darstellt.

Zurück zum Inhaltsverzeichnis