3.2 Transkritische Bifurkation

 

Um eine Vorstellung der transkritischen Bifurkation zu erhalten, geht man genauso vor, wie bei der Sattel-Knoten-Bifurkation, zuerst betrachten wir ein dynamisches System: 

 

  ,

 

die Differentialgleichung vom nichtlinearen Typ wird eine Stufe komplizierter gewählt, das ist der Typ von Differentialgleichung (in Normalform), bei dem transkritische Bifurkationen auftreten:

 

                                                         .

 

Wiederum gesucht sind nun die stationären Lösungen der Differentialgleichung, um Aussagen über deren Stabilitätsverhalten treffen zu können.

 

Die stationäre Lösung ist gegeben durch:

 

        

                                      Û    

                                      Û                

 

Für diese Fixpunkte ist die lineare Stabilitätsuntersuchung durchzuführen. Im allgemeinen Fall lautet die linearisierte Differentialgleichung für kleine Auslenkungen :

 

 

 

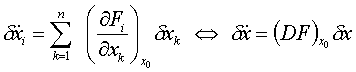
Für den vorliegenden Fall ergibt sich also:

 

 

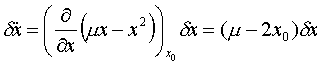
und somit für die Determinante der Jakobi-Matrix der Ausdruck

, das Problem ist eindimensional.

 

Betrachten wir nun den 1. Fixpunkt und die zugehörige, linearisierte Differentialgleichung:

 

                                     

    

 

Die allgemeine Lösung dieser linearisierten Differentialgleichung lautet:

                           

 

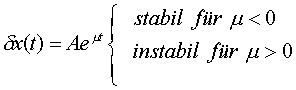
Für den 2. Fixpunkt und die zugehörige, linearisierte Differentialgleichung ergibt sich:        

                                       

      

 

Die allgemeine Lösung dieser linearisierten Differentialgleichung lautet:

                           

 

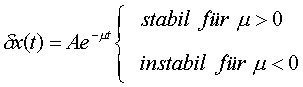
Der Fixpunkt  ist also stabil für m > 0 (stabiler Knoten) und instabil für m < 0 (Sattelpunkt).

 

Der Fixpunkt  hingegen ist stabil für m < 0 (stabiler Knoten) und instabil für m > 0 (Sattelpunkt).

 

Mathematisch anschaulich läßt sich dieses Ergebnis wieder mit den anschwellenden und abklingenden Exponentialfunktionen in Abhängigkeit vom Vorzeichen des Kontrollparameters m herleiten. Die so erhaltenen Ergebnisse stimmen mit der Klassifikation der Fixpunkte mittels Linearer Stabilitätsanalyse überein.

Im Parameterraum ergibt sich damit folgendes Bild:

 

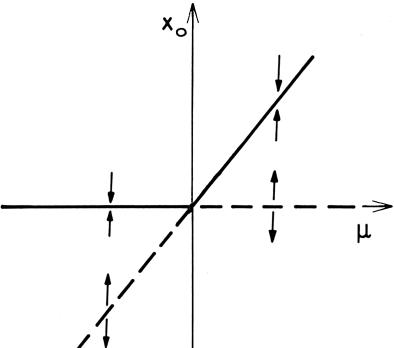
Ein Sattelpunkt und ein stabiler Knoten vereinigen und trennen sich wieder. Am Bifurkationspunkt  überschneiden sich die Graphen des ersten und zweiten Fixpunktes (lat. trans – über, jenseits), daher der Name: transkritische Bifurkation.

 

Während des Seminarvortrags wurde ein Beispiel aus der Anwendung, der Laser, genannt: Hier ist "x" die emittierte Photonenzahl.

Unterhalb der Laserschwelle, also für m < 0, gibt es keine Verstärkung, der Ast  ist stabil, der instabile Ast fehlt allerdings, da es keine negative Verstärkung gibt. Oberhalb der Laserschwelle, also für m > 0, wird der Ast stabil, es gibt Verstärkung. Der Ast , also der Bereich ohne Verstärkung, wird instabil.